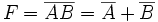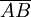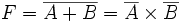Los circuitos digitales son componentes de hardware que manipulan información binaria. Los circuitos se construyen con partes electrónicas como transistores diodos y resistores. Cada circuito recibe el nombre de compuerta la cual realiza una operacion lógica específica y la salida de una compuerta se puede aplicar a la entrada de otras compuertas para formar el circuito digital requerido.
Para describir la propiedades operacionales de los circuitos digitales, es necesario presentar el sistema matemático llamado álgebra booleana en honor del matemático ingles George Boole que especifica la operación de cada compuerta.
El álgebra booleana se utiliza para desccribir la interconexión de compuertas digitales y para transformar diagramas de circiuos en expresiones algebráicas.
Lógica Binaria
La lógica binaria tiene que ver con variales que asumen dos valores discretos y operaciones que asumen un significado lógico. Los dos valores que toman las variables son 1 y 0 y su nombre es designado por letras del alfabeto.
Existen 3 operaciones logicas asociadas con los valores binarios llamada "and", "or", "not"
AND. esta oparecion se representa por un punto o por la ausencia de un operador, por ejemplo:
x·y=z
xy=z (se lee x y y igual a z)
La operacion lógica AND se interpreta con z=1 si y sólo si x=1 y y=1, de lo contrario z=0.
OR. esta operación está representada por un signo +, por ejemplo:
x+y=z (se lee x o y igual a z)
NOT. esta operación se representa por medio de una barracolocada arriba de una variable. Se conoce también como operación complemento porque cambia un 1 por 0 y 0 por 1.
Compuertas Lógicas
Son circuitos electrónicos que operan con 1 o más señales de entrada para producir una señal de salida.
Los símbolos gráficos que se utilizan para designar los 3 tipos de compuerta son:
Las compuertas son bloques de hardware qe producen el equivalente de señales de salida 1 y 0 lógicos si se satisfacen requicitos de lógica de entrada. La señales de entrada x y y pueden existir en las compuertas AND y OR en uno de los 4 estados posibles 00, 01, 10, 11.
Las compuertas AND y OR pueden tener mas de dos entradas. la compuerta AND de 3 entradas responde con una salida de un 1 lógico si las 3 entradas son 1, de lo contrario la salida sera 0. la compuerta OR de 4 entradas responde con un 1 logico si alguna netrada es 1 de lo contrario su salida se convierte en 0.
Álgebra
una funcion booleana espresa la relacion logica entre variables binarias, se evalua determinando el valor binario de la expreseion de todos los valores posibles de las variables.